Easter Egg decorating and hunting are without a doubt the most popular Easter tradition. Although it’s not 100% clear where it all began, a popular theory about the origin of Easter eggs, according to Carole Levin, professor of history and director of the Medieval and Renaissance Studies Program at the University of Nebraska, eggs were a part of an Anglo-Saxon festival that celebrated the goddess Eastre.
It doesn’t matter where it started, because during the month of April it’s impossible to miss the colourful symbols of life and renewal. Whether they are hand-dyed or filled with chocolate, it’s a mark of Easter to get a basketful during an Easter Egg Hunt.
In any high-stakes Easter Egg Hunt, there is bound to be some misfortune. Could be someone in a rush stomping on an egg they failed to notice. It might be the case of too many eggs in one basket. Just how much can an average egg take before it finds itself halfway to an omelet?
We ran simulations through our Irazu software to find the answers to keep as many of the eggs intact as possible.
Simulating the eggs
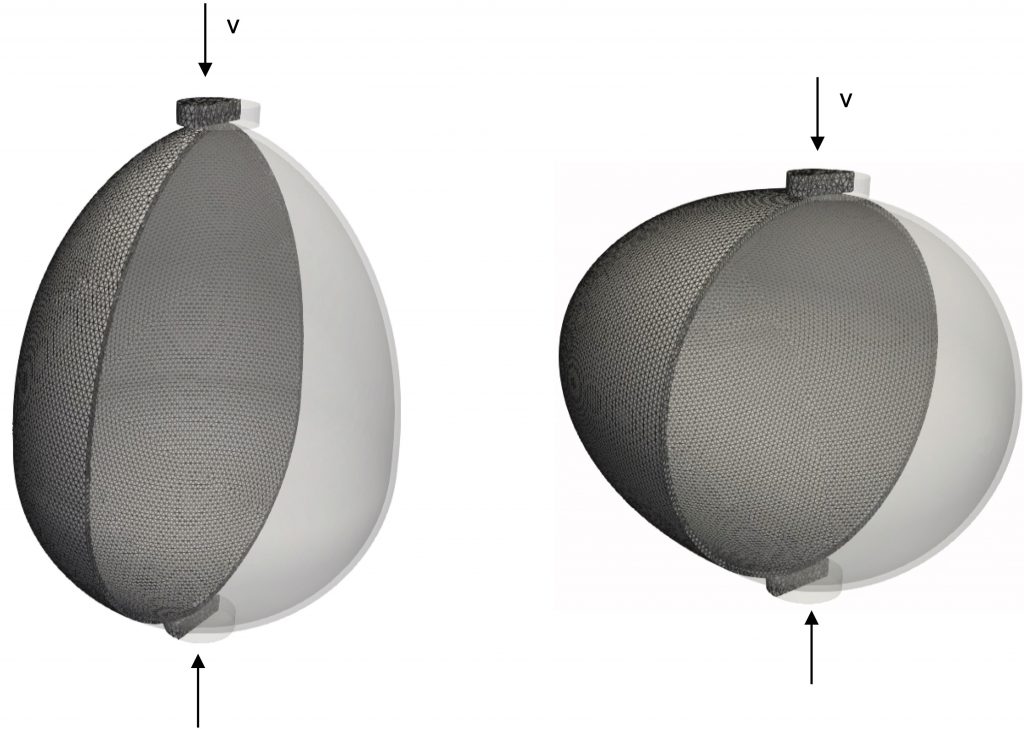
The team began by building a three-dimensional (3D) model of a typical egg measuring 55 mm in length and 40 mm in width with a thickness of about 0.6 mm. The eggs were loaded by applying constant velocities to two thin cylinders placed at the top and bottom of the egg. The model geometries were discretized by a tetrahedral finite element mesh (approximately 188,000 elements in total). The egg shell material was modelled as a brittle, isotropic solid and assigned suitable stiffness and strength property values.
Results
The simulated fracturing of the eggs loaded in two directions is highlighted in the model animations below. Failure initiates as crushing of the eggshell under the loading platens. Under increasing pressure, tensile fractures start to nucleate and grow around the entire perimeter of the eggs. Most of this damage occurs after reaching the peak load.
The eggs begin to crack and break as pressure from the loading platens increases for loading along the long axis.
The eggs begin to crack and break as pressure from the loading platens increases for loading along the short axis.
The force required to break the eggs was derived from the analysis of the reactionary forces acting on the loading platens as a function of the vertical displacement of these platens. As shown in the graph below, peak applied forces of 45.2 N (4.6 kg) and 20.8 N (2.1 kg) were recorded for loading along the long and short axis. These are the forces required to break the egg in each direction. These forces correspond well with those reported in the literature [e.g., 1, 2].
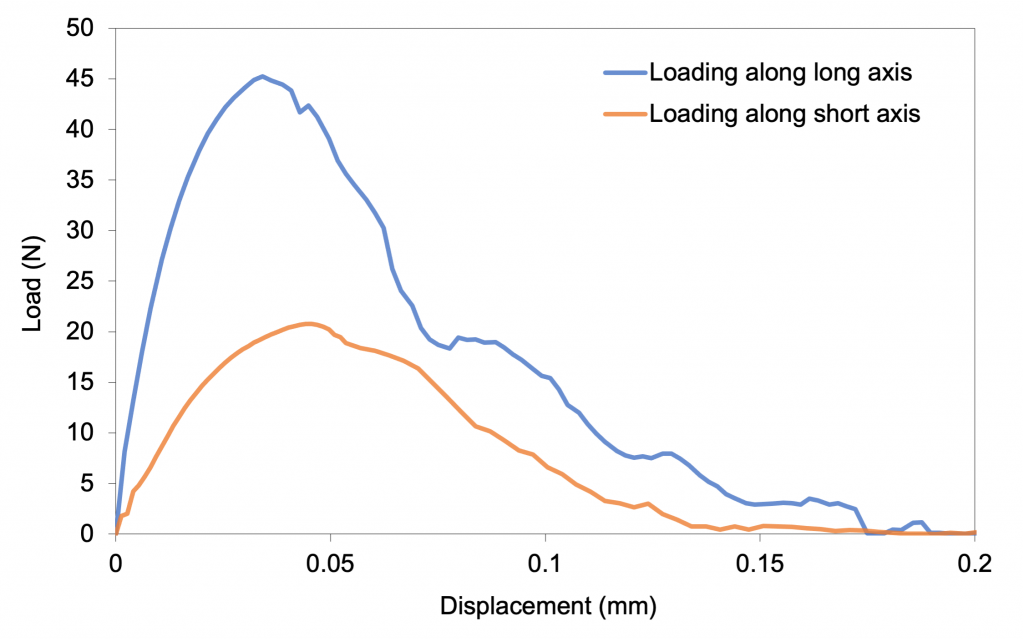
This Easter, we want you to have the best chance possible at getting the most intact eggs in your basket. As you can see, the vertical loading of the egg is over twice as strong as the horizontal loading. For most favourable results, ensure you are loading them in a vertical arrangement to ensure the strongest possible base for your mountain of eggs. We hope you have a safe and happy Easter.