Understanding and predicting the the rock mass mechanical response to temperature variations is relevant for a number of geo-engineering applications, including: underground disposal of nuclear waste, geothermal energy extraction, underground LNG storage, geological sequestration of CO2, and coal bed gas extraction.

We are pleased to announce that we have been working on the introduction of thermo-mechanical coupling in our FEMDEM software and will take this opportunity to present some preliminary results. Similar to the approach implemented in other commercial geomechanical packages, the adopted modelling strategy is based on a one-way-coupled thermo-elastic model. That is, variations in the temperature field are related to the mechanical deformation through a thermal expansion coefficient. As the temperature in the rock changes, the resulting expansion or contraction can produce thermally-induced stresses depending on the applied boundary conditions and the heterogeneity of the temperature field and thermal properties within the rock. If these stresses are sufficiently high, the rock can become damaged.

As an example, we consider a 300-mm-diameter disc with a 30-mm-diameter circular hole in the centre. The material is assumed to be homogeneous and isotropic with stiffness and strength property values typical of a brittle hard rock. The thermal expansion coefficient, α_t, is equal to 10E-6°C^-1. The disc is assumed to be entirely unconstrained with a uniform initial temperature of 20°C.

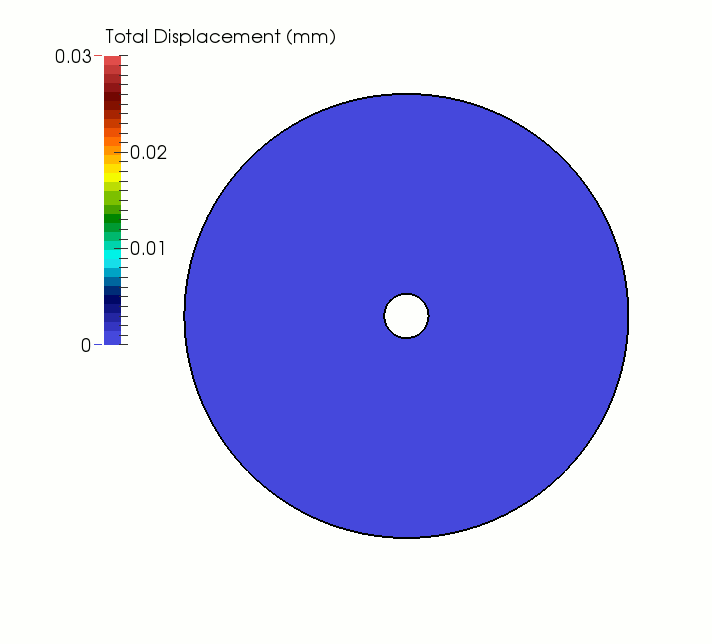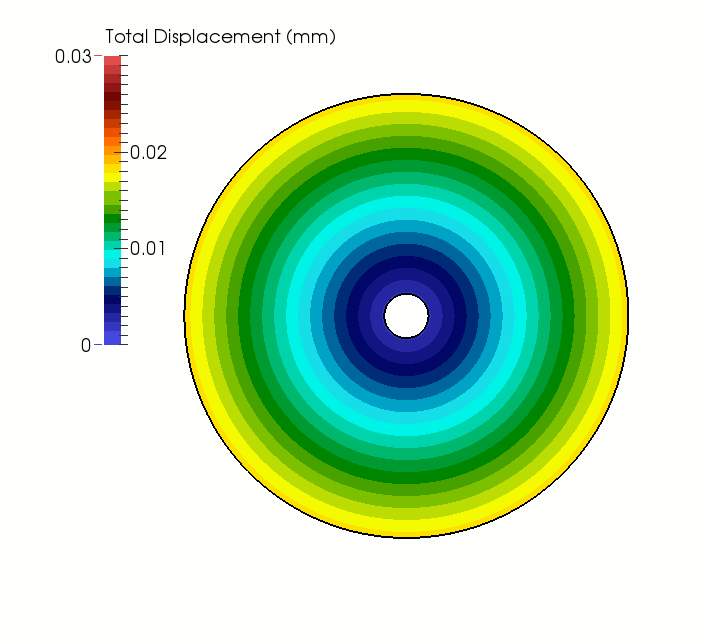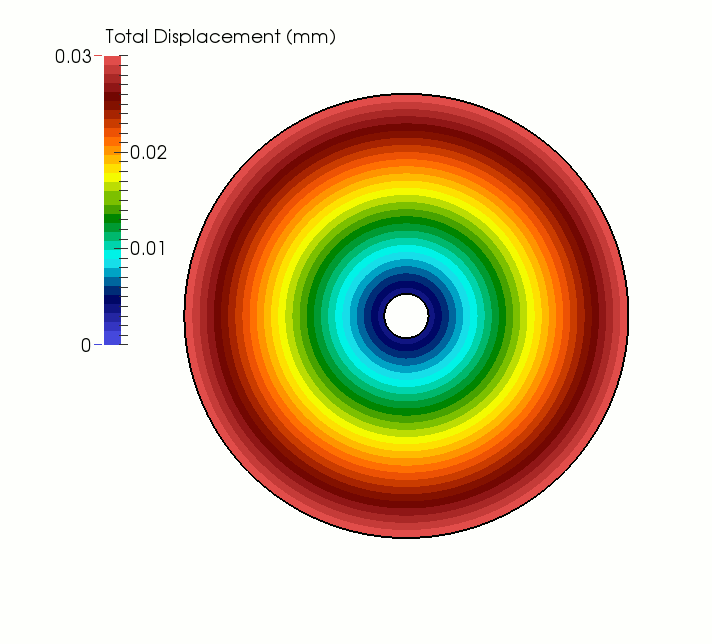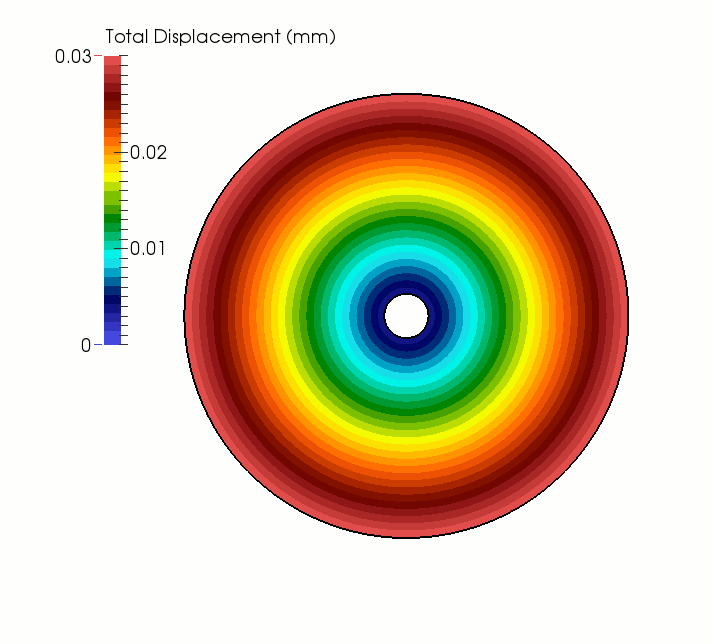
In a first simulation case, the temperature throughout the disc is gradually increased from to 20°C to 40°C and then held constant. As shown in the animation below, as the disc is heated, it expands radially outward and increases in volume. Upon reaching equilibrium, points located on the outer boundary experience a displacement of 0.03 mm, which is equal to the theoretical value computed as ΔT R_e α_t (where ΔT = 20°C is the total temperature increment and R_e = 150 mm is the outer radius of the specimen). With the exception of some low-magnitude temporary stress arising during the heating phase due to inertial effects, no stresses develop in the model.

Evolution of displacement field for a uniformly heated, unconstrained hollow disc.

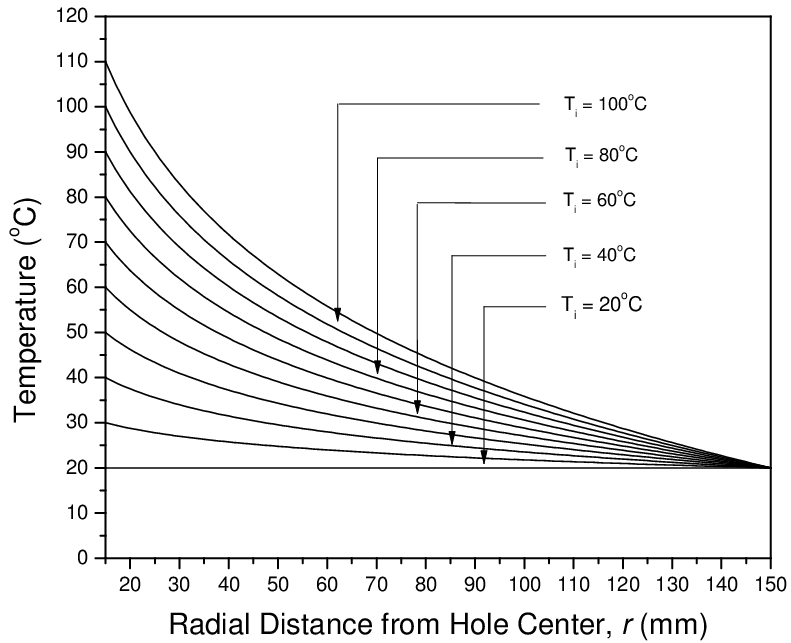
In a second simulation case, the same hollow disc is subjected to a gradual increase of the inner temperature, T_i, from 20°C to 120°C, while the outer temperature is held constant at 20°C. The resulting temperature distribution between the inner and outer boundary that is applied to the model is determined analytically according to the figure below.

Steady-state temperature distribution inside the hollow disc for increasing values of the inner temperature.

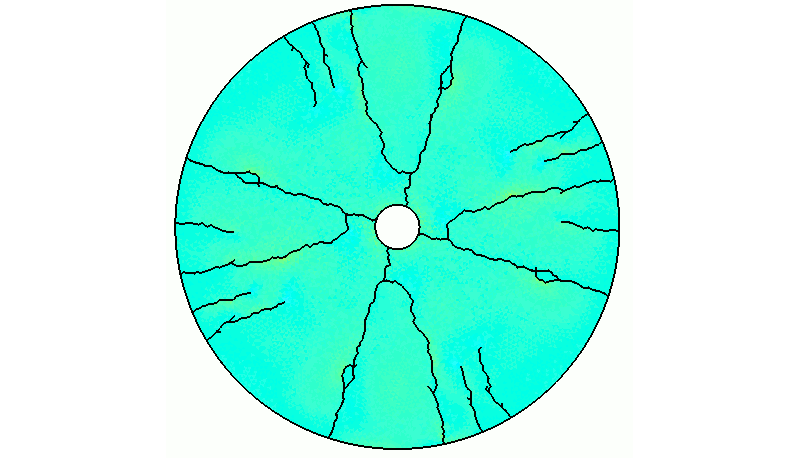
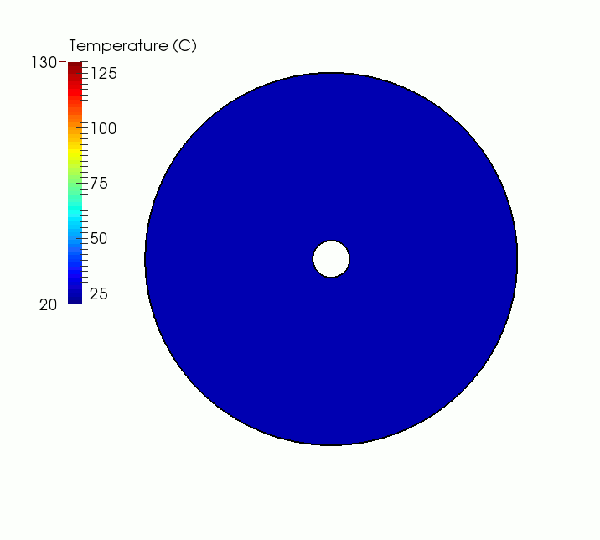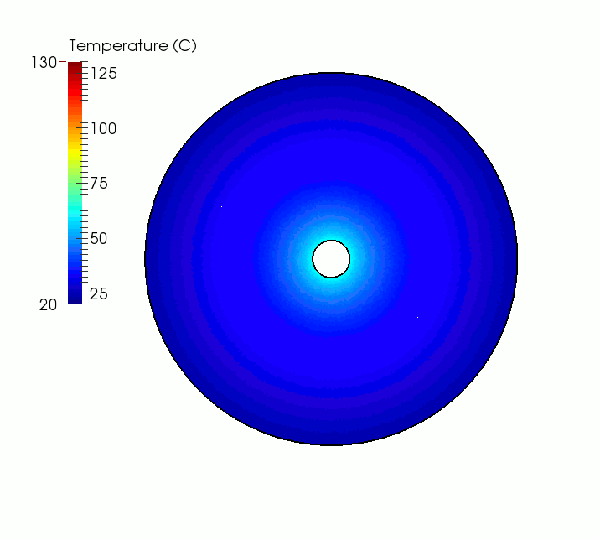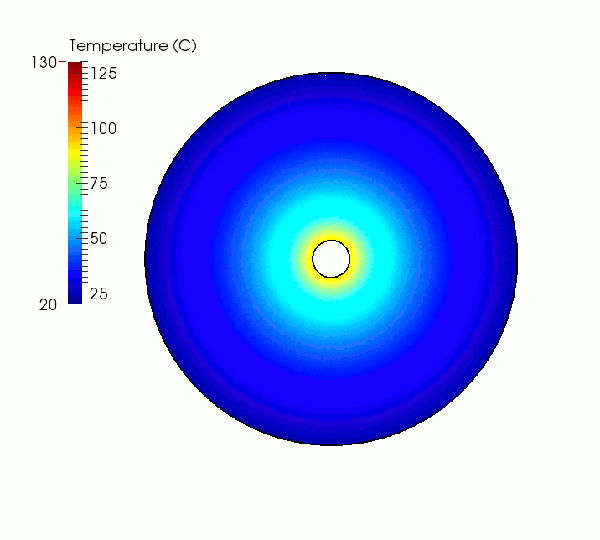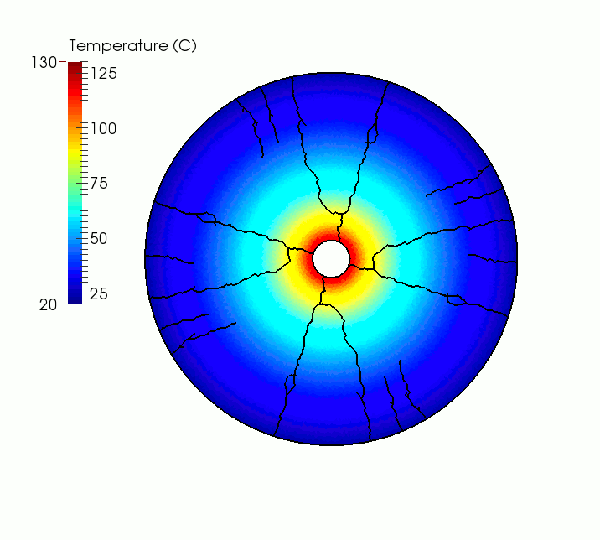
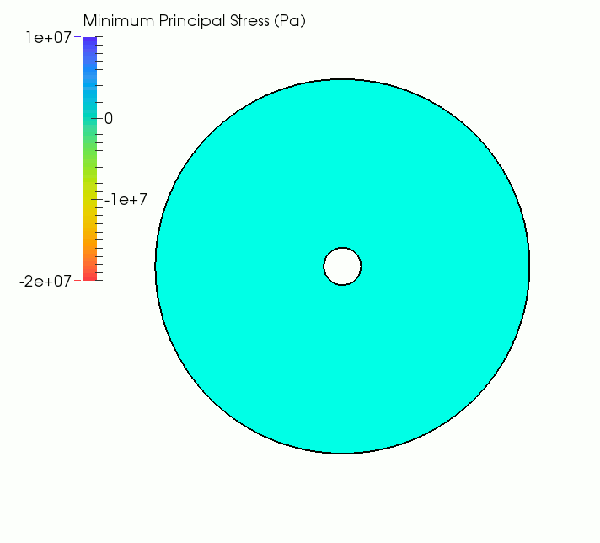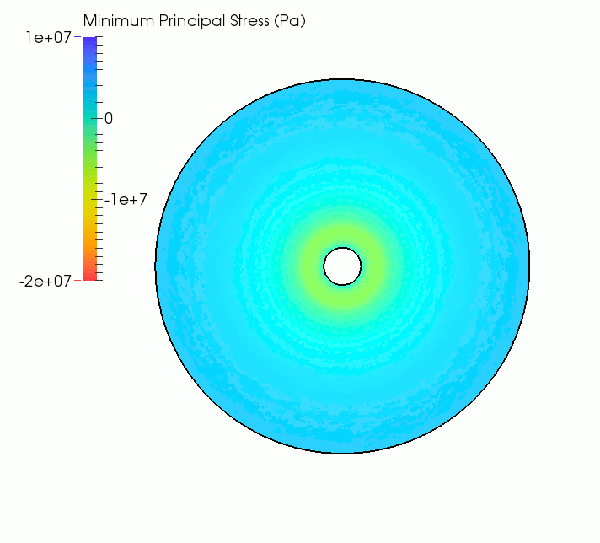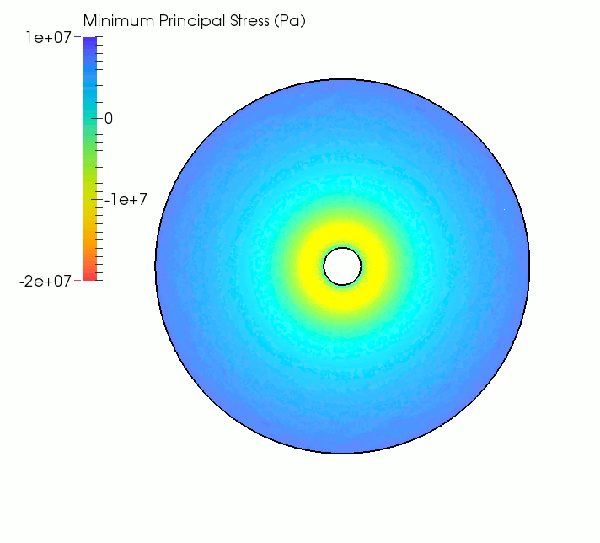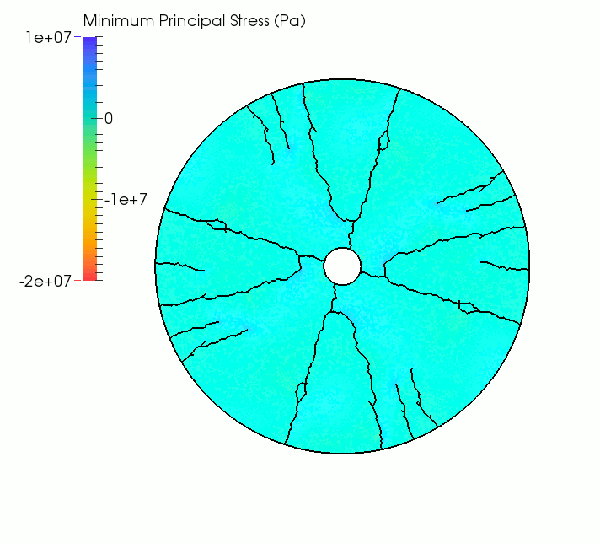
As highlighted in the simulation sequences below, the increasing thermal gradient causes the development of tensile and compressive stresses at the outer and inner model boundary, respectively. When the inner temperature reaches approximately 105°C the tensile hoop stresses generated in the cooler outer portions of the specimen overcome the tensile strength of the rock (~9 MPa). As a result, macroscopic tensile fractures nucleate and propagate radially towards the specimen center.

Simulated temperature field evolution.

Simulated evolution of maximum principal stress.

Simulated evolution of minimum principal stress.